응력은 수직응력과 전단응력으로 재질면적에서 수직, 평행 방향의 응력만 존재한다.
그렇다면 대각선 방향에서 힘이 들어오거나, 재료를 대각선으로 잘라 그 평면에서 발생하는 응력을 해석하려면?
무슨말인지 모르겠지요. 그림을 보자.

위의 그림과 같이 점선에 따라 재료를 자르면 새로운 평면이 생기고, 이 비스듬한 평면에서 발생하는 응력을 재해석해보는 것이다.
응력을 귀찮게 조합해서 풀어야하니 이번단원의 명칭은 조합응력이다.
일단 원래발생한 힘을 평면에 따라 재풀이한다.
즉 Fx의 힘이 대각평면에서는 수직힘으로 Fx*cos(a)가 된다.
응력=힘/면적이므로, 면적은 대각평면이 더 크므로 원래단면 A를 cos(a)로 나눈값이 된다.
이 부분이 이해가 안간다면 삼각함수를 다시 공부하도록 합시다.
그럼 새로 자른 평면에서 수직응력은 Fx*cos(a)*cos(a)/A가 된다.
Fx/A를 기존응력 시그마라고 하면, 시그마*cos^2(a)가 되는 것이다.
이번엔 전단응력을 봐보자.
같은 과정으로
대각평면에서의 수평힘 Fx*sin(a) 면적 A/cos(a)이다.
즉 전단응력은 시그마*sin(a)*cos(a)이다.
sin(a)*cos(a)는 삼각함수의 반각공식에 의해 1/2sin(2a)가 된다.
이것도 삼각함수 파트인데 반각공식이니 뭐니 굳이 안외워도 되긴하다.
왜냐하면 곧 나올 모어원을 통해 쉽게 유도할 수 있기 때문이다.
여하튼 1축응력을 제멋대로 자른 평면에서 수직, 전단응력으로 새로 해석해보았다.
2축응력도 있고, 3축응력도 있다.
그럼 구하기가 매우 귀찮아질 것이다.
그래서 나온게 모어원이라는 개념이다.
바로 그림먼저 봐보자~
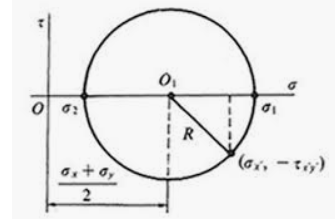
x축은 시그마(수직응력), y축은 타우(전단응력)으로 놓는다.
그리고 기본조건으로 주어진 수직응력중 큰값을 오른쪽에 찍고, 작은값을 왼쪽에 찍고 원을 만들자.
모어원 완성이다.
만약 1축응력이라서 작은 값이 없다면요??
없는게 아니라 0으로 놓으면 된다.
그럼 원점에서 시작하는 원형이 되겠지..
그리고 원하는 각도로 원점에서 쭉 선을 잇고, 원과 닿는 접점에서 시그마, 타우 값을 계산하면 그것이 조합응력이 된다.
하지만 여기서 주의할 점이 있다. 모어원에서는 2배의 각을 찍어야 한다는 것이다.
예를 들어 재료를 x축기준으로 30도 비스듬히 자른 평면의 조합응력값을 알고 싶다면
모어원에서는 x축기준으로 반시계 방향으로 60도만큼 두배의 각을 돌려서 잘라야 한다는 것이다.
왜 모어원에서는 각을 두배로 취급해야하나요?
라고 물을수 있다. 원리를 포스팅하려면 피곤하므로 간단한 예를 통해 이해하도록하자.
1축응력을 예에서 90도로 평면을 자른다고 생각해보자. 그렇다면 결국 기존과 같은 평면이 되는 것이다.
그렇다면 전단응력 또한 애초에 없어야 겠지.. 그럼 이번엔 모어원을 살펴보자.
위 그림의 모어원에서 전단응력이 없으려면 x축과 접점이 되어야한다.
이제 이해했으리라 본다. 원리적으로 보면 두 쌍을 지니기 때문에 반원을 큰 원으로 확대해서 해석하기 떄문이라고만 알면 될 것이다. 그냥 간단한 예로 이해하는게 편하다.
1축, 2축은 모어원으로 간단히 해석이 되고 평면응력이라고 2축 수직응력과 전단응력이 함께 발생할 때,
조합응력을 보는 경우가 있다.
위에서 모어원을 그릴 때 수직응력 두개의 값을 x축에 찍고 원 만들었는데, 이런 경우는 x축이 아닌 전단응력값도
고려하여 오른쪽은 x축 위, 왼쪽으로 x축 아래 (반대로 해도 상관X) 찍고 원을 돌리면 된다.
여기서 주응력(순수하게 수직응력만 발생하는 응력)평면을 살펴보면 기존에 주어진 수직응력 값보다 크게 된다.
기존에 주어진 전단응력이 수직응력쪽으로 가기 때문에. 원을 그리고 연필로 돌려보면 쉽게 이해될 것이다.
그 값의 크기는 따로 유도하지 않겠다.
이상으로 조합응력과 모어원파트를 끝내며..
공식집으로만 보면 sin, cos 어쩌고 저쩌고 하면서 식이 많다.
식을 그대로 외우려고 한다면 미련한 행동이다.
모어원을 쓰지 않고 외우기로 한다면 어떤 원리로 이런식이 나왔는지 알아야 나중에 활용할 수가 있다.
그냥 지저분한 공식을 외우면, 외우기도 힘들뿐더러, 적용하기도 쉽지 않으니
모어원을 적극 활용하는 것을 추천한다.
'재료역학' 카테고리의 다른 글
| [재료역학]6장.비틀림 (0) | 2020.03.04 |
|---|---|
| [재료역학]5장.평면도형의 성질 (0) | 2020.03.03 |
| [재료역학]3장.열응력, 탄성에너지 (2) | 2020.02.27 |
| [재료역학]2장.변형률 (0) | 2020.02.26 |
| [정역학]기초이론 (0) | 2020.02.25 |
